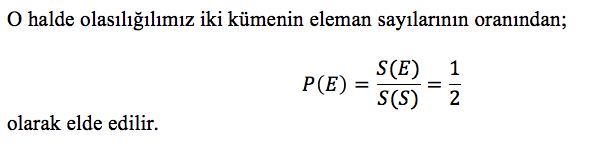İnsanoğlunun tarih boyunca en çok merak ettiği şey nedir? Bu soruya farklı cevaplar verilebilir, ancak çoğunlukla “gelecekte ne olacağı” merak edilir. Bunun yansıması olarak da karşımıza geleceğe yolculuk, gelecekteki araçlara dair öngörüler, yeni buluşların gelecekte ne işe yarayacağı gibi birçok kurgu çıkar. Geçmişten gelen yol tektir ancak gelecek birçok yol ayrımına sahiptir ve karar gerektiren her ayrımın sonuçları belirsizdir. İşte bilim alanlarında belirsizliğin olduğu yerde matematik, matematikte de “olasılık” çıkar karşımıza.
Modern olasılık kuramının temellerinin 16. ve 17. yüzyıllarda atıldığını söylemek yanlış olmaz. Nüfusu hızla artan dünyada bir sonraki yılın ihtiyaçlarını belirleme ve ekonomik öngörülerde bulunma zorunluluğu matematik ve olasılığın gelişmesini sağlamıştır. Günümüzde matematik ve olasılık vazgeçilmezlerimiz arasında yerini almıştır. Siz hissetmeseniz de etrafınızdaki birçok olay, olasılık hesapları temelinde gerçekleşir. Birkaç örnek vermek gerekirse;
- Şehir içinde trafik ışıklarının yanma sırasının ve süresinin belirlenmesi,
- Şehir içinde kullandığımız otobüslerin hangi sıklıkta sefer yapacağı,
- Petrol, altın ve döviz değerlerinin tahmini,
- Bankaların ve şirketlerin müşteri hizmetlerini aradığımızda müşteri temsilcisine bağlanmak için ne kadar bekleyeceğimizin ya da müşteri hizmetlerinde telefonlara cevap verecek kaç kişinin çalışması gerektiğinin belirlenmesi,
- Eldeki verilerle hava durumu tahmini,
gibi olayların birçoğu ön araştırma ve verilerle elde edilenlerin olasılık açısından değerlendirilmesi ile gerçekleşir. Şu an hemen hemen her bilim dalında kullanılan olasılık, birçok alanda araştırmaların temelini oluşturuyor.
Peki, öğrencilerin öğrenmekte zorluk çektiği olasılık hesapları nasıl yapılır, neden tutar ya da tutmaz? Olasılık şans mıdır?
Olasılık temel olarak gerçekleşme durumlarının incelenmesi ile ilgilenir. Ayrıca şans değil, bilimsel temeli olan bir tahmin demektir. “Parayı 10 kez havaya attım, 8 kez yazı geldi. Eğer olasılık 1/2 ise 5 kez yazı gelmesi gerekmez mi?” sorusu, genç öğrencilerimden gelen ve mantıklı olduğuna inandıkları bir sorudur. Ama bu soruda gözden kaçırılan en önemli nokta, olasılığın gerçekleşmiş olaylar üzerinden kurgulanmadığıdır. Olasılık gerçekleşmesi olası olaylar üzerinden kurulur, yani geçmişe değil geleceğe dair tahmini değerler verir.
Bir olayın gerçekleşme olasılığını belirlemek için, o olayın gerçekleştiği örneklem uzayının tüm bileşenlerini bilmeniz gerekir. Örneğin bir futbol maçını A takımının kazanma olasılığını (takımların eşit güçte olduğunu düşünelim) bilmek istiyorsanız futbolun kurallarını ya da maçın kaç durumla sonuçlanacağını bilmek zorundasınız. Futbolda üç sonuç vardır; ya A kazanır ya B kazanır ya da berabere biter ki biz tüm durumların kümesine örneklem uzay diyoruz. Doğal olarak bu olaylardan birinin gerçekleşme olasılığı 1/3 olacaktır. Ama siz bunu tenis için düşünürseniz örneklem uzayınız ya A kazanır ya da B kazanır şeklinde olacak, kazanma ihtimali ise 1/2 olarak elde edilecektir. O halde olasılığı belirlemek için olayı ve olayın ait olduğu örneklem uzayı tanımalıyız.
Şimdi sorumuza dönelim. Bir madeni para havaya atıldığında yazı gelme olasılığı neden 1/2 ’dir?
Yukarıdaki tanım gereği durumu matematiksel boyutta inceleyelim. S örnek uzayımız olduğuna göre;
S = {Yazı, Tura}
olay kümemiz E için;
E = {Yazı}
Peki, biz bu olasılık hesabının gerçek hayatta da geçerli olduğunu nereden bilebiliriz?
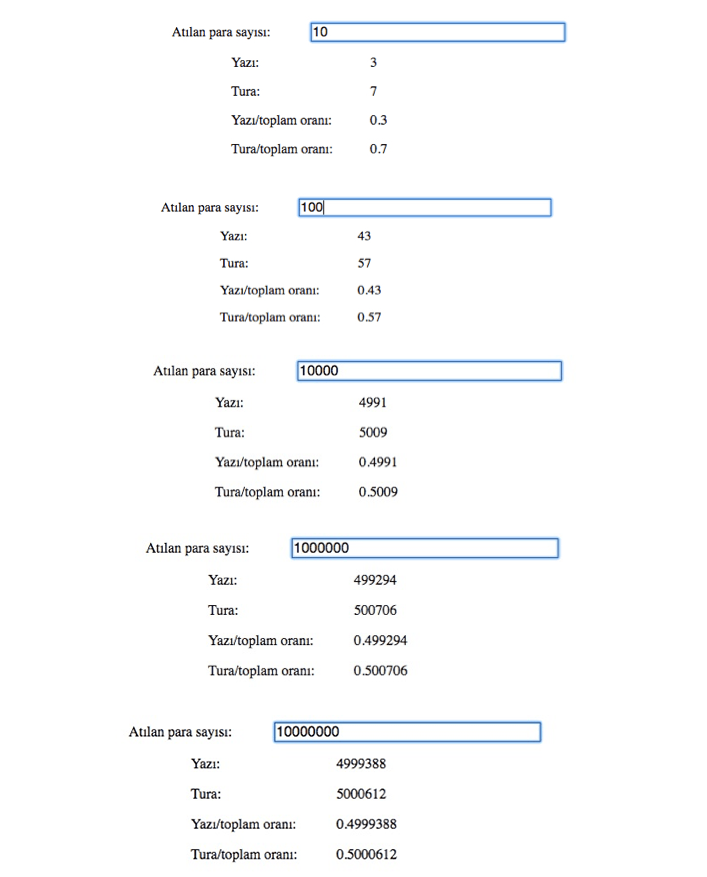
Bunun için Scratch ve HTML tabanlı yazdığımız farklı iki bilgisayar programından faydalanabiliriz. Örneğin HTML tabanlı yazdığımız programda parayı sırasıyla 10, 100, 10.000, 1.000.000 ve 10.000.000 kez havaya attığımızı farz edelim. Gerekli verileri programa girdiğimizde, rastgele gelen yazı-tura sayısını ve olasılıkları gösteren aşağıdaki sonuçlarla karşılaşırız.
Ne görüyorsunuz? Yazı-tura olasılıkları atış sayısının artmasıyla nasıl değişti?
Aslında denemelerde bulduğumuz şey olasılık değildir. Yani siz bir parayı havaya kaç kez atarsanız atın, atış sayısının yarısı kadar yazı veya tura gelmek zorunda değildir. Matematik size durumun en iyi modellemesini sunar, yani sonucun 1/2 = 0,5 olduğunu verir. Bu değer, atışı sonsuz kez tekrarladığınızda ortaya çıkacak sonuçtur. İşte matematiğin en güzel yanlarından biri! Hiç ulaşamayacağınız bir deneme sayısının sonucunu akıl yürüterek elde edebiliyorsunuz.
Şimdi size http://www.virtualcointoss.com/ sitesini önereceğim. Siteye girip “Flip” düğmesine tıkladığınızda parayı bir kez havaya atmış oluyorsunuz. Şu ana kadar 24.272.936 (sayı her gün artıyor) kez para atışı yapılmış ve bunların 12.140.648 tanesi yazı gelmiş. İki değeri oranladığınızda ortaya çıkan sayı 0,50017221 yani yazı gelme olasılığı neredeyse 1/2 = 0,5 !
Siz de Scratch ve HTML tabanlı yazdığımız bilgisayar programlarından faydalanarak farklı denemeler gerçekleştirebilirsiniz. İsterseniz yazacağınız bir programla “Zarın asal sayı gelme olasılığı kaçtır?” gibi sorulara da cevap verebilirsiniz.
Matematikle ve sevgiyle kalın!
Not: Programın yazılması sırasında yardımlarından ötürü, şu an birer yazılımcı olan değerli öğrencilerim Melih Yasin Yalçın ve Onur Selek’e teşekkür ederim.
BİLİM GENÇ Yrd. Doç. Dr. Burak Karabey 16.03.2017